In Depth Tutorial

Note: Many of the concepts explained here, are also covered in the mlr3book.

Parameters (using paradox)

The paradox package offers a language for the description of parameter spaces, as well as tools for useful operations on these parameter spaces. A parameter space is often useful when describing:

A set of sensible input values for an R function
The set of possible values that slots of a configuration object can take
The search space of an optimization process

The tools provided by paradox therefore relate to:

Parameter checking: Verifying that a set of parameters satisfies the conditions of a parameter space
Parameter sampling: Generating parameter values that lie in the parameter space for systematic exploration of program behavior depending on these parameters

paradox is, by nature, an auxiliary package that derives its usefulness from other packages that make use of it. It is heavily utilized in other mlr-org packages such as mlr3, mlr3pipelines, and mlr3tuning.

Reference Based Objects

paradox is the spiritual successor to the ParamHelpers package and was written from scratch using the R6 class system. The most important consequence of this is that all objects created in paradox are “reference-based”, unlike most other objects in R. When a change is made to a ParamSet object, for example by adding a parameter using the $add() function, all variables that point to this ParamSet will contain the changed object. To create an independent copy of a ParamSet, the $clone() method needs to be used:

library("paradox")

ps = ParamSet$new()
ps2 = ps
ps3 = ps$clone(deep = TRUE)
print(ps) # the same for ps2 and ps3

## <ParamSet>
## Empty.

ps$add(ParamLgl$new("a"))

print(ps)  # ps was changed

## <ParamSet>
##    id    class lower upper nlevels        default value
## 1:  a ParamLgl    NA    NA       2 <NoDefault[3]>

print(ps2) # contains the same reference as ps

## <ParamSet>
##    id    class lower upper nlevels        default value
## 1:  a ParamLgl    NA    NA       2 <NoDefault[3]>

print(ps3) # is a "clone" of the old (empty) ps

## <ParamSet>
## Empty.

Defining a Parameter Space

Single Parameters

The basic building block for describing parameter spaces is the Param class. It represents a single parameter, which usually can take a single atomic value. Consider, for example, trying to configure the rpart package’s rpart.control object. It has various components (minsplit, cp, …) that all take a single value, and that would all be represented by a different instance of a Param object.

The Param class has various subclasses that represent different value types:

ParamInt: Integer numbers
ParamDbl: Real numbers
ParamFct: String values from a set of possible values, similar to R factors
ParamLgl: Truth values (TRUE / FALSE), as logicals in R
ParamUty: Parameter that can take any value

A particular instance of a parameter is created by calling the attached $new() function:

library("paradox")
parA = ParamLgl$new(id = "A")
parB = ParamInt$new(id = "B", lower = 0, upper = 10, tags = c("tag1", "tag2"))
parC = ParamDbl$new(id = "C", lower = 0, upper = 4, special_vals = list(NULL))
parD = ParamFct$new(id = "D", levels = c("x", "y", "z"), default = "y")
parE = ParamUty$new(id = "E", custom_check = function(x) checkmate::checkFunction(x))

Every parameter must have:

id - A name for the parameter within the parameter set
default - A default value
special_vals - A list of values that are accepted even if they do not conform to the type
tags - Tags that can be used to organize parameters

The numeric (Int and Dbl) parameters furthermore allow for specification of a lower and upper bound. Meanwhile, the Fct parameter must be given a vector of levels that define the possible states its parameter can take. The Uty parameter can also have a custom_check function that must return TRUE when a value is acceptable and may return a character(1) error description otherwise. The example above defines parE as a parameter that only accepts functions.

All values which are given to the constructor are then accessible from the object for inspection using $. Although all these values can be changed for a parameter after construction, this can be a bad idea and should be avoided when possible.

Instead, a new parameter should be constructed. Besides the possible values that can be given to a constructor, there are also the $class, $nlevels, $is_bounded, $has_default, $storage_type, $is_number and $is_categ slots that give information about a parameter.

A list of all slots can be found in ?Param.

parB$lower

## [1] 0

parA$levels

## [1]  TRUE FALSE

parE$class

## [1] "ParamUty"

It is also possible to get all information of a Param as data.table by calling as.data.table().

as.data.table(parA)

##    id    class lower upper      levels nlevels is_bounded special_vals
## 1:  A ParamLgl    NA    NA  TRUE,FALSE       2       TRUE    <list[0]>
##           default storage_type tags
## 1: <NoDefault[3]>      logical

Type / Range Checking

A Param object offers the possibility to check whether a value satisfies its condition, i.e. is of the right type, and also falls within the range of allowed values, using the $test(), $check(), and $assert() functions. test() should be used within conditional checks and returns TRUE or FALSE, while check() returns an error description when a value does not conform to the parameter (and thus plays well with the "checkmate::assert()" function). assert() will throw an error whenever a value does not fit.

parA$test(FALSE)

## [1] TRUE

parA$test("FALSE")

## [1] FALSE

parA$check("FALSE")

## [1] "Must be of type 'logical flag', not 'character'"

Instead of testing single parameters, it is often more convenient to check a whole set of parameters using a ParamSet.

Parameter Sets

The ordered collection of parameters is handled in a ParamSet¹. It is initialized using the $new() function and optionally takes a list of Params as argument. Parameters can also be added to the constructed ParamSet using the $add() function. It is even possible to add whole ParamSets to other ParamSets.

ps = ParamSet$new(list(parA, parB))
ps$add(parC)
ps$add(ParamSet$new(list(parD, parE)))
print(ps)

## <ParamSet>
##    id    class lower upper nlevels        default value
## 1:  A ParamLgl    NA    NA       2 <NoDefault[3]>      
## 2:  B ParamInt     0    10      11 <NoDefault[3]>      
## 3:  C ParamDbl     0     4     Inf <NoDefault[3]>      
## 4:  D ParamFct    NA    NA       3              y      
## 5:  E ParamUty    NA    NA     Inf <NoDefault[3]>

The individual parameters can be accessed through the $params slot. It is also possible to get information about all parameters in a vectorized fashion using mostly the same slots as for individual Params (i.e. $class, $levels etc.), see ?ParamSet for details.

It is possible to reduce ParamSets using the $subset method. Be aware that it modifies a ParamSet in-place, so a “clone” must be created first if the original ParamSet should not be modified.

psSmall = ps$clone()
psSmall$subset(c("A", "B", "C"))
print(psSmall)

## <ParamSet>
##    id    class lower upper nlevels        default value
## 1:  A ParamLgl    NA    NA       2 <NoDefault[3]>      
## 2:  B ParamInt     0    10      11 <NoDefault[3]>      
## 3:  C ParamDbl     0     4     Inf <NoDefault[3]>

Just as for Params, and much more useful, it is possible to get the ParamSet as a data.table using as.data.table(). This makes it easy to subset parameters on certain conditions and aggregate information about them, using the variety of methods provided by data.table.

as.data.table(ps)

##    id    class lower upper      levels nlevels is_bounded special_vals
## 1:  A ParamLgl    NA    NA  TRUE,FALSE       2       TRUE    <list[0]>
## 2:  B ParamInt     0    10                  11       TRUE    <list[0]>
## 3:  C ParamDbl     0     4                 Inf       TRUE    <list[1]>
## 4:  D ParamFct    NA    NA       x,y,z       3       TRUE    <list[0]>
## 5:  E ParamUty    NA    NA                 Inf      FALSE    <list[0]>
##           default storage_type      tags
## 1: <NoDefault[3]>      logical          
## 2: <NoDefault[3]>      integer tag1,tag2
## 3: <NoDefault[3]>      numeric          
## 4:              y    character          
## 5: <NoDefault[3]>         list

Type / Range Checking

Similar to individual Params, the ParamSet provides $test(), $check() and $assert() functions that allow for type and range checking of parameters. Their argument must be a named list with values that are checked against the respective parameters. It is possible to check only a subset of parameters.

ps$check(list(A = TRUE, B = 0, E = identity))

## [1] TRUE

ps$check(list(A = 1))

## [1] "A: Must be of type 'logical flag', not 'double'"

ps$check(list(Z = 1))

## [1] "Parameter 'Z' not available. Did you mean 'A' / 'B' / 'C'?"

Values in a `ParamSet`

Although a ParamSet fundamentally represents a value space, it also has a slot $values that can contain a point within that space. This is useful because many things that define a parameter space need similar operations (like parameter checking) that can be simplified. The $values slot contains a named list that is always checked against parameter constraints. When trying to set parameter values, e.g. for mlr3 Learners, it is the $values slot of its $param_set that needs to be used.

ps$values = list(A = TRUE, B = 0)
ps$values$B = 1
print(ps$values)

## $A
## [1] TRUE
## 
## $B
## [1] 1

The parameter constraints are automatically checked:

ps$values$B = 100

## Error in self$assert(xs): Assertion on 'xs' failed: B: Element 1 is not <= 10.

Dependencies

It is often the case that certain parameters are irrelevant or should not be given depending on values of other parameters. An example would be a parameter that switches a certain algorithm feature (for example regularization) on or off, combined with another parameter that controls the behavior of that feature (e.g. a regularization parameter). The second parameter would be said to depend on the first parameter having the value TRUE.

A dependency can be added using the $add_dep method, which takes both the ids of the “depender” and “dependee” parameters as well as a Condition object. The Condition object represents the check to be performed on the “dependee”. Currently it can be created using CondEqual$new() and CondAnyOf$new(). Multiple dependencies can be added, and parameters that depend on others can again be depended on, as long as no cyclic dependencies are introduced.

The consequence of dependencies are twofold: For one, the $check(), $test() and $assert() tests will not accept the presence of a parameter if its dependency is not met. Furthermore, when sampling or creating grid designs from a ParamSet, the dependencies will be respected.

The following example makes parameter D depend on parameter A being FALSE, and parameter B depend on parameter D being one of "x" or "y". This introduces an implicit dependency of B on A being FALSE as well, because D does not take any value if A is TRUE.

ps$add_dep("D", "A", CondEqual$new(FALSE))
ps$add_dep("B", "D", CondAnyOf$new(c("x", "y")))

ps$check(list(A = FALSE, D = "x", B = 1))          # OK: all dependencies met

## [1] TRUE

ps$check(list(A = FALSE, D = "z", B = 1))          # B's dependency is not met

## [1] "The parameter 'B' can only be set if the following condition is met 'D ∈ {x, y}'. Instead the current parameter value is: D=z"

ps$check(list(A = FALSE, B = 1))                   # B's dependency is not met

## [1] "The parameter 'B' can only be set if the following condition is met 'D ∈ {x, y}'. Instead the parameter value for 'D' is not set at all. Try setting 'D' to a value that satisfies the condition"

ps$check(list(A = FALSE, D = "z"))                 # OK: B is absent

## [1] TRUE

ps$check(list(A = TRUE))                           # OK: neither B nor D present

## [1] TRUE

ps$check(list(A = TRUE, D = "x", B = 1))           # D's dependency is not met

## [1] "The parameter 'D' can only be set if the following condition is met 'A = FALSE'. Instead the current parameter value is: A=TRUE"

ps$check(list(A = TRUE, B = 1))                    # B's dependency is not met

## [1] "The parameter 'B' can only be set if the following condition is met 'D ∈ {x, y}'. Instead the parameter value for 'D' is not set at all. Try setting 'D' to a value that satisfies the condition"

Internally, the dependencies are represented as a data.table, which can be accessed listed in the $deps slot. This data.table can even be mutated, to e.g. remove dependencies. There are no sanity checks done when the $deps slot is changed this way. Therefore it is advised to be cautious.

ps$deps

##    id on           cond
## 1:  D  A <CondEqual[9]>
## 2:  B  D <CondAnyOf[9]>

Vector Parameters

Unlike in the old ParamHelpers package, there are no more vectorial parameters in paradox. Instead, it is now possible to create multiple copies of a single parameter using the $rep function. This creates a ParamSet consisting of multiple copies of the parameter, which can then (optionally) be added to another ParamSet.

ps2d = ParamDbl$new("x", lower = 0, upper = 1)$rep(2)
print(ps2d)

## <ParamSet>
##         id    class lower upper nlevels        default value
## 1: x_rep_1 ParamDbl     0     1     Inf <NoDefault[3]>      
## 2: x_rep_2 ParamDbl     0     1     Inf <NoDefault[3]>

ps$add(ps2d)
print(ps)

## <ParamSet>
##         id    class lower upper nlevels        default parents value
## 1:       A ParamLgl    NA    NA       2 <NoDefault[3]>          TRUE
## 2:       B ParamInt     0    10      11 <NoDefault[3]>       D     1
## 3:       C ParamDbl     0     4     Inf <NoDefault[3]>              
## 4:       D ParamFct    NA    NA       3              y       A      
## 5:       E ParamUty    NA    NA     Inf <NoDefault[3]>              
## 6: x_rep_1 ParamDbl     0     1     Inf <NoDefault[3]>              
## 7: x_rep_2 ParamDbl     0     1     Inf <NoDefault[3]>

It is also possible to use a ParamUty to accept vectorial parameters, which also works for parameters of variable length. A ParamSet containing a ParamUty can be used for parameter checking, but not for sampling. To sample values for a method that needs a vectorial parameter, it is advised to use a parameter transformation function that creates a vector from atomic values.

Assembling a vector from repeated parameters is aided by the parameter’s $tags: Parameters that were generated by the $rep() command automatically get tagged as belonging to a group of repeated parameters.

ps$tags

## $A
## character(0)
## 
## $B
## [1] "tag1" "tag2"
## 
## $C
## character(0)
## 
## $D
## character(0)
## 
## $E
## character(0)
## 
## $x_rep_1
## [1] "x_rep"
## 
## $x_rep_2
## [1] "x_rep"

Parameter Sampling

It is often useful to have a list of possible parameter values that can be systematically iterated through, for example to find parameter values for which an algorithm performs particularly well (tuning). paradox offers a variety of functions that allow creating evenly-spaced parameter values in a “grid” design as well as random sampling. In the latter case, it is possible to influence the sampling distribution in more or less fine detail.

A point to always keep in mind while sampling is that only numerical and factorial parameters that are bounded can be sampled from, i.e. not ParamUty. Furthermore, for most samplers ParamInt and ParamDbl must have finite lower and upper bounds.

Parameter Designs

Functions that sample the parameter space fundamentally return an object of the Design class. These objects contain the sampled data as a data.table under the $data slot, and also offer conversion to a list of parameter-values using the $transpose() function.

Grid Design

The generate_design_grid() function is used to create grid designs that contain all combinations of parameter values: All possible values for ParamLgl and ParamFct, and values with a given resolution for ParamInt and ParamDbl. The resolution can be given for all numeric parameters, or for specific named parameters through the param_resolutions parameter.

design = generate_design_grid(psSmall, 2)
print(design)

## <Design> with 8 rows:
##        A  B C
## 1:  TRUE  0 0
## 2:  TRUE  0 4
## 3:  TRUE 10 0
## 4:  TRUE 10 4
## 5: FALSE  0 0
## 6: FALSE  0 4
## 7: FALSE 10 0
## 8: FALSE 10 4

generate_design_grid(psSmall, param_resolutions = c(B = 1, C = 2))

## <Design> with 4 rows:
##    B C     A
## 1: 0 0  TRUE
## 2: 0 0 FALSE
## 3: 0 4  TRUE
## 4: 0 4 FALSE

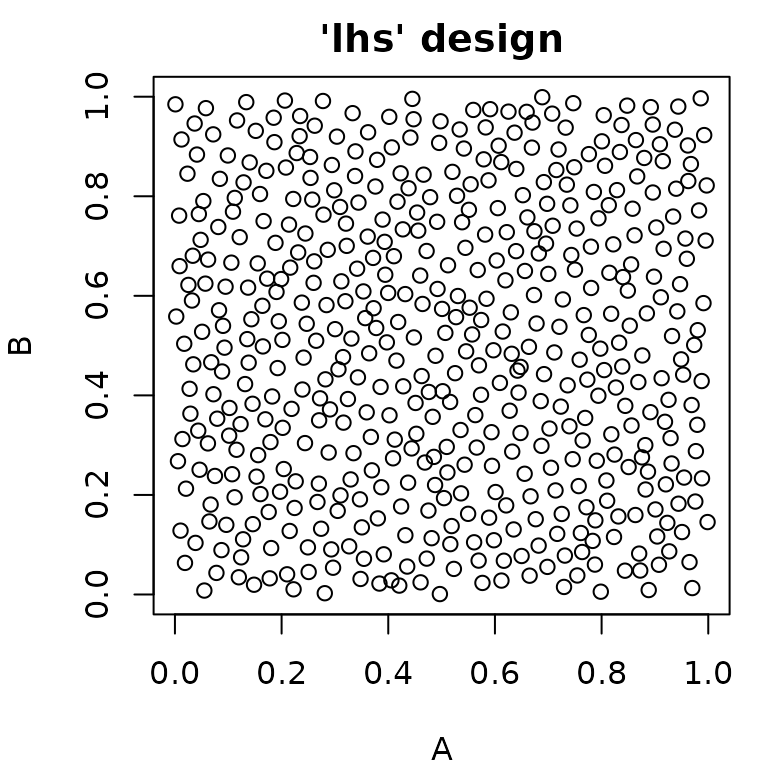
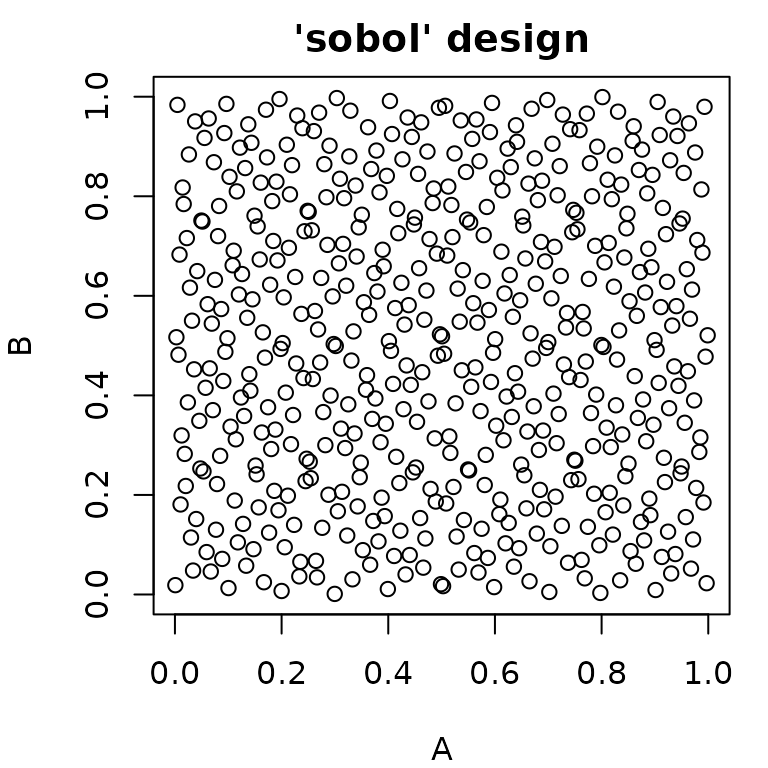
Random Sampling

paradox offers different methods for random sampling, which vary in the degree to which they can be configured. The easiest way to get a uniformly random sample of parameters is generate_design_random(). It is also possible to create “latin hypercube” sampled parameter values using generate_design_lhs(), which utilizes the lhs package. LHS-sampling creates low-discrepancy sampled values that cover the parameter space more evenly than purely random values.

pvrand = generate_design_random(ps2d, 500)
pvlhs = generate_design_lhs(ps2d, 500)

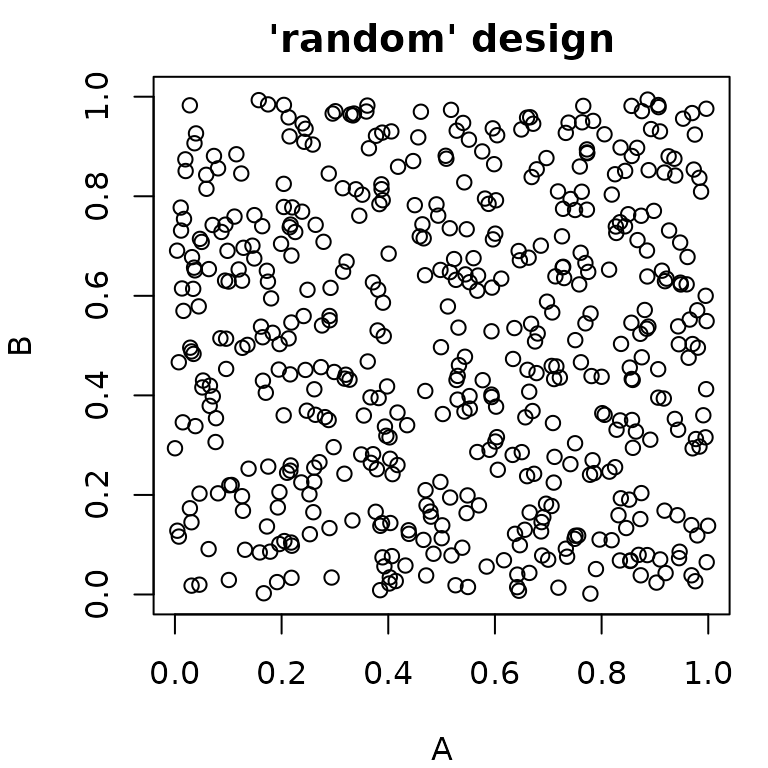
Generalized Sampling: The `Sampler` Class

It may sometimes be desirable to configure parameter sampling in more detail. paradox uses the Sampler abstract base class for sampling, which has many different sub-classes that can be parameterized and combined to control the sampling process. It is even possible to create further sub-classes of the Sampler class (or of any of its subclasses) for even more possibilities.

Every Sampler object has a sample() function, which takes one argument, the number of instances to sample, and returns a Design object.

1D-Samplers

There is a variety of samplers that sample values for a single parameter. These are Sampler1DUnif (uniform sampling), Sampler1DCateg (sampling for categorical parameters), Sampler1DNormal (normally distributed sampling, truncated at parameter bounds), and Sampler1DRfun (arbitrary 1D sampling, given a random-function). These are initialized with a single Param, and can then be used to sample values.

sampA = Sampler1DCateg$new(parA)
sampA$sample(5)

## <Design> with 5 rows:
##        A
## 1:  TRUE
## 2: FALSE
## 3: FALSE
## 4:  TRUE
## 5: FALSE

Hierarchical Sampler

The SamplerHierarchical sampler is an auxiliary sampler that combines many 1D-Samplers to get a combined distribution. Its name “hierarchical” implies that it is able to respect parameter dependencies. This suggests that parameters only get sampled when their dependencies are met.

The following example shows how this works: The Int parameter B depends on the Lgl parameter A being TRUE. A is sampled to be TRUE in about half the cases, in which case B takes a value between 0 and 10. In the cases where A is FALSE, B is set to NA.

psSmall$add_dep("B", "A", CondEqual$new(TRUE))
sampH = SamplerHierarchical$new(psSmall,
  list(Sampler1DCateg$new(parA),
    Sampler1DUnif$new(parB),
    Sampler1DUnif$new(parC))
)
sampled = sampH$sample(1000)
table(sampled$data[, c("A", "B")], useNA = "ifany")

##        B
## A         0   1   2   3   4   5   6   7   8   9  10 <NA>
##   FALSE   0   0   0   0   0   0   0   0   0   0   0  507
##   TRUE   52  34  52  43  32  45  44  49  42  40  60    0

Joint Sampler

Another way of combining samplers is the SamplerJointIndep. SamplerJointIndep also makes it possible to combine Samplers that are not 1D. However, SamplerJointIndep currently can not handle ParamSets with dependencies.

sampJ = SamplerJointIndep$new(
  list(Sampler1DUnif$new(ParamDbl$new("x", 0, 1)),
    Sampler1DUnif$new(ParamDbl$new("y", 0, 1)))
)
sampJ$sample(5)

## <Design> with 5 rows:
##            x         y
## 1: 0.0663621 0.9311695
## 2: 0.0701956 0.6745297
## 3: 0.5386720 0.8731148
## 4: 0.3090126 0.3447093
## 5: 0.5831048 0.9276041

SamplerUnif

The Sampler used in generate_design_random() is the SamplerUnif sampler, which corresponds to a HierarchicalSampler of Sampler1DUnif for all parameters.

Parameter Transformation

While the different Samplers allow for a wide specification of parameter distributions, there are cases where the simplest way of getting a desired distribution is to sample parameters from a simple distribution (such as the uniform distribution) and then transform them. This can be done by assigning a function to the $trafo slot of a ParamSet. The $trafo function is called with two parameters:

The list of parameter values to be transformed as x
The ParamSet itself as param_set

The $trafo function must return a list of transformed parameter values.

The transformation is performed when calling the $transpose function of the Design object returned by a Sampler with the trafo ParamSet to TRUE (the default). The following, for example, creates a parameter that is exponentially distributed:

psexp = ParamSet$new(list(ParamDbl$new("par", 0, 1)))
psexp$trafo = function(x, param_set) {
  x$par = -log(x$par)
  x
}
design = generate_design_random(psexp, 2)
print(design)

## <Design> with 2 rows:
##          par
## 1: 0.7127069
## 2: 0.5247303

design$transpose()  # trafo is TRUE

## [[1]]
## [[1]]$par
## [1] 0.338685
## 
## 
## [[2]]
## [[2]]$par
## [1] 0.6448708

Compare this to $transpose() without transformation:

design$transpose(trafo = FALSE)

## [[1]]
## [[1]]$par
## [1] 0.7127069
## 
## 
## [[2]]
## [[2]]$par
## [1] 0.5247303

Transformation between Types

Usually the design created with one ParamSet is then used to configure other objects that themselves have a ParamSet which defines the values they take. The ParamSets which can be used for random sampling, however, are restricted in some ways: They must have finite bounds, and they may not contain “untyped” (ParamUty) parameters. $trafo provides the glue for these situations. There is relatively little constraint on the trafo function’s return value, so it is possible to return values that have different bounds or even types than the original ParamSet. It is even possible to remove some parameters and add new ones.

Suppose, for example, that a certain method requires a function as a parameter. Let’s say a function that summarizes its data in a certain way. The user can pass functions like median() or mean(), but could also pass quantiles or something completely different. This method would probably use the following ParamSet:

methodPS = ParamSet$new(
  list(
    ParamUty$new("fun",
      custom_check = function(x) checkmate::checkFunction(x, nargs = 1))
  )
)
print(methodPS)

## <ParamSet>
##     id    class lower upper nlevels        default value
## 1: fun ParamUty    NA    NA     Inf <NoDefault[3]>

If one wanted to sample this method, using one of four functions, a way to do this would be:

samplingPS = ParamSet$new(
  list(
    ParamFct$new("fun", c("mean", "median", "min", "max"))
  )
)

samplingPS$trafo = function(x, param_set) {
  # x$fun is a `character(1)`,
  # in particular one of 'mean', 'median', 'min', 'max'.
  # We want to turn it into a function!
  x$fun = get(x$fun, mode = "function")
  x
}

design = generate_design_random(samplingPS, 2)
print(design)

## <Design> with 2 rows:
##     fun
## 1:  min
## 2: mean

Note that the Design only contains the column “fun” as a character column. To get a single value as a function, the $transpose function is used.

xvals = design$transpose()
print(xvals[[1]])

## $fun
## function (..., na.rm = FALSE)  .Primitive("min")

We can now check that it fits the requirements set by methodPS, and that fun it is in fact a function:

methodPS$check(xvals[[1]])

## [1] TRUE

xvals[[1]]$fun(1:10)

## [1] 1

Imagine now that a different kind of parametrization of the function is desired: The user wants to give a function that selects a certain quantile, where the quantile is set by a parameter. In that case the $transpose function could generate a function in a different way. For interpretability, the parameter is called “quantile” before transformation, and the “fun” parameter is generated on the fly.

samplingPS2 = ParamSet$new(
  list(
    ParamDbl$new("quantile", 0, 1)
  )
)

samplingPS2$trafo = function(x, param_set) {
  # x$quantile is a `numeric(1)` between 0 and 1.
  # We want to turn it into a function!
  list(fun = function(input) quantile(input, x$quantile))
}

design = generate_design_random(samplingPS2, 2)
print(design)

## <Design> with 2 rows:
##      quantile
## 1: 0.14670249
## 2: 0.03183454

The Design now contains the column “quantile” that will be used by the $transpose function to create the fun parameter. We also check that it fits the requirement set by methodPS, and that it is a function.

xvals = design$transpose()
print(xvals[[1]])

## $fun
## function(input) quantile(input, x$quantile)
## <environment: 0x556191971270>

methodPS$check(xvals[[1]])

## [1] TRUE

xvals[[1]]$fun(1:10)

## 14.67025% 
##  2.320322

Defining a Tuning Spaces

When running an optimization, it is important to inform the tuning algorithm about what hyperparameters are valid. Here the names, types, and valid ranges of each hyperparameter are important. All this information is communicated with objects of the class ParamSet, which is defined in paradox. While it is possible to create ParamSet-objects using its $new-constructor, it is much shorter and readable to use the ps-shortcut, which will be presented here.

Note, that ParamSet objects exist in two contexts. First, ParamSet-objects are used to define the space of valid parameter settings for a learner (and other objects). Second, they are used to define a search space for tuning. We are mainly interested in the latter. For example we can consider the minsplit parameter of the mlr_learners_classif.rpart", "classif.rpart Learner. The ParamSet associated with the learner has a lower but no upper bound. However, for tuning the value, a lower and upper bound must be given because tuning search spaces need to be bounded. For Learner or PipeOp objects, typically “unbounded” ParamSets are used. Here, however, we will mainly focus on creating “bounded” ParamSets that can be used for tuning.

Creating `ParamSet`s

An empty "ParamSet – not yet very useful – can be constructed using just the "ps" call:

search_space = ps()
print(search_space)

## <ParamSet>
## Empty.

ps takes named Domain arguments that are turned into parameters. A possible search space for the "classif.svm" learner could for example be:

search_space = ps(
  cost = p_dbl(lower = 0.1, upper = 10),
  kernel = p_fct(levels = c("polynomial", "radial"))
)
print(search_space)

## <ParamSet>
##        id    class lower upper nlevels        default value
## 1:   cost ParamDbl   0.1    10     Inf <NoDefault[3]>      
## 2: kernel ParamFct    NA    NA       2 <NoDefault[3]>

There are five domain constructors that produce a parameters when given to ps:

Constructor	Description	Is bounded?	Underlying Class
`p_dbl`	Real valued parameter (“double”)	When `upper` and `lower` are given	`ParamDbl`
`p_int`	Integer parameter	When `upper` and `lower` are given	`ParamInt`
`p_fct`	Discrete valued parameter (“factor”)	Always	`ParamFct`
`p_lgl`	Logical / Boolean parameter	Always	`ParamLgl`
`p_uty`	Untyped parameter	Never	`ParamUty`

These domain constructors each take some of the following arguments:

lower, upper: lower and upper bound of numerical parameters (p_dbl and p_int). These need to be given to get bounded parameter spaces valid for tuning.
levels: Allowed categorical values for p_fct parameters. Required argument for p_fct. See below for more details on this parameter.
trafo: transformation function, see below.
depends: dependencies, see below.
tags: Further information about a parameter, used for example by the hyperband tuner.
default: Value corresponding to default behavior when the parameter is not given. Not used for tuning search spaces.
special_vals: Valid values besides the normally accepted values for a parameter. Not used for tuning search spaces.
custom_check: Function that checks whether a value given to p_uty is valid. Not used for tuning search spaces.

The lower and upper parameters are always in the first and second position respectively, except for p_fct where levels is in the first position. It is preferred to omit the labels (ex: upper = 0.1 becomes just 0.1). This way of defining a ParamSet is more concise than the equivalent definition above. Preferred:

search_space = ps(cost = p_dbl(0.1, 10), kernel = p_fct(c("polynomial", "radial")))

Transformations (`trafo`)

We can use the paradox function generate_design_grid to look at the values that would be evaluated by grid search. (We are using rbindlist() here because the result of $transpose() is a list that is harder to read. If we didn’t use $transpose(), on the other hand, the transformations that we investigate here are not applied.) In generate_design_grid(search_space, 3), search_space is the ParamSet argument and 3 is the specified resolution in the parameter space. The resolution for categorical parameters is ignored; these parameters always produce a grid over all of their valid levels. For numerical parameters the endpoints of the params are always included in the grid, so if there were 3 levels for the kernel instead of 2 there would be 9 rows, or if the resolution was 4 in this example there would be 8 rows in the resulting table.

library("data.table")
rbindlist(generate_design_grid(search_space, 3)$transpose())

##     cost     kernel
## 1:  0.10 polynomial
## 2:  0.10     radial
## 3:  5.05 polynomial
## 4:  5.05     radial
## 5: 10.00 polynomial
## 6: 10.00     radial

We notice that the cost parameter is taken on a linear scale. We assume, however, that the difference of cost between 0.1 and 1 should have a similar effect as the difference between 1 and 10. Therefore it makes more sense to tune it on a logarithmic scale. This is done by using a transformation (trafo). This is a function that is applied to a parameter after it has been sampled by the tuner. We can tune cost on a logarithmic scale by sampling on the linear scale [-1, 1] and computing 10^x from that value.

search_space = ps(
  cost = p_dbl(-1, 1, trafo = function(x) 10^x),
  kernel = p_fct(c("polynomial", "radial"))
)
rbindlist(generate_design_grid(search_space, 3)$transpose())

##    cost     kernel
## 1:  0.1 polynomial
## 2:  0.1     radial
## 3:  1.0 polynomial
## 4:  1.0     radial
## 5: 10.0 polynomial
## 6: 10.0     radial

It is even possible to attach another transformation to the ParamSet as a whole that gets executed after individual parameter’s transformations were performed. It is given through the .extra_trafo argument and should be a function with parameters x and param_set that takes a list of parameter values in x and returns a modified list. This transformation can access all parameter values of an evaluation and modify them with interactions. It is even possible to add or remove parameters. (The following is a bit of a silly example.)

search_space = ps(
  cost = p_dbl(-1, 1, trafo = function(x) 10^x),
  kernel = p_fct(c("polynomial", "radial")),
  .extra_trafo = function(x, param_set) {
    if (x$kernel == "polynomial") {
      x$cost = x$cost * 2
    }
    x
  }
)
rbindlist(generate_design_grid(search_space, 3)$transpose())

##    cost     kernel
## 1:  0.2 polynomial
## 2:  0.1     radial
## 3:  2.0 polynomial
## 4:  1.0     radial
## 5: 20.0 polynomial
## 6: 10.0     radial

The available types of search space parameters are limited: continuous, integer, discrete, and logical scalars. There are many machine learning algorithms, however, that take parameters of other types, for example vectors or functions. These can not be defined in a search space ParamSet, and they are often given as ParamUty in the Learner’s ParamSet. When trying to tune over these hyperparameters, it is necessary to perform a Transformation that changes the type of a parameter.

An example is the class.weights parameter of the Support Vector Machine (SVM), which takes a named vector of class weights with one entry for each target class. The trafo that would tune class.weights for the tsk("spam") dataset could be:

search_space = ps(
  class.weights = p_dbl(0.1, 0.9, trafo = function(x) c(spam = x, nonspam = 1 - x))
)
generate_design_grid(search_space, 3)$transpose()

## [[1]]
## [[1]]$class.weights
##    spam nonspam 
##     0.1     0.9 
## 
## 
## [[2]]
## [[2]]$class.weights
##    spam nonspam 
##     0.5     0.5 
## 
## 
## [[3]]
## [[3]]$class.weights
##    spam nonspam 
##     0.9     0.1

(We are omitting rbindlist() in this example because it breaks the vector valued return elements.)

Automatic Factor Level Transformation

A common use-case is the necessity to specify a list of values that should all be tried (or sampled from). It may be the case that a hyperparameter accepts function objects as values and a certain list of functions should be tried. Or it may be that a choice of special numeric values should be tried. For this, the p_fct constructor’s level argument may be a value that is not a character vector, but something else. If, for example, only the values 0.1, 3, and 10 should be tried for the cost parameter, even when doing random search, then the following search space would achieve that:

search_space = ps(
  cost = p_fct(c(0.1, 3, 10)),
  kernel = p_fct(c("polynomial", "radial"))
)
rbindlist(generate_design_grid(search_space, 3)$transpose())

##    cost     kernel
## 1:  0.1 polynomial
## 2:  0.1     radial
## 3:  3.0 polynomial
## 4:  3.0     radial
## 5: 10.0 polynomial
## 6: 10.0     radial

This is equivalent to the following:

search_space = ps(
  cost = p_fct(c("0.1", "3", "10"),
    trafo = function(x) list(`0.1` = 0.1, `3` = 3, `10` = 10)[[x]]),
  kernel = p_fct(c("polynomial", "radial"))
)
rbindlist(generate_design_grid(search_space, 3)$transpose())

##    cost     kernel
## 1:  0.1 polynomial
## 2:  0.1     radial
## 3:  3.0 polynomial
## 4:  3.0     radial
## 5: 10.0 polynomial
## 6: 10.0     radial

Note: Though the resolution is 3 here, in this case it doesn’t matter because both cost and kernel are factors (the resolution for categorical variables is ignored, these parameters always produce a grid over all their valid levels).

This may seem silly, but makes sense when considering that factorial tuning parameters are always character values:

search_space = ps(
  cost = p_fct(c(0.1, 3, 10)),
  kernel = p_fct(c("polynomial", "radial"))
)
typeof(search_space$params$cost$levels)

## [1] "character"

Be aware that this results in an “unordered” hyperparameter, however. Tuning algorithms that make use of ordering information of parameters, like genetic algorithms or model based optimization, will perform worse when this is done. For these algorithms, it may make more sense to define a p_dbl or p_int with a more fitting trafo.

The class.weights case from above can also be implemented like this, if there are only a few candidates of class.weights vectors that should be tried. Note that the levels argument of p_fct must be named if there is no easy way for as.character() to create names:

search_space = ps(
  class.weights = p_fct(
    list(
      candidate_a = c(spam = 0.5, nonspam = 0.5),
      candidate_b = c(spam = 0.3, nonspam = 0.7)
    )
  )
)
generate_design_grid(search_space)$transpose()

## [[1]]
## [[1]]$class.weights
##    spam nonspam 
##     0.5     0.5 
## 
## 
## [[2]]
## [[2]]$class.weights
##    spam nonspam 
##     0.3     0.7

Parameter Dependencies (`depends`)

Some parameters are only relevant when another parameter has a certain value, or one of several values. The Support Vector Machine (SVM), for example, has the degree parameter that is only valid when kernel is "polynomial". This can be specified using the depends argument. It is an expression that must involve other parameters and be of the form <param> == <scalar>, <param> %in% <vector>, or multiple of these chained by &&. To tune the degree parameter, one would need to do the following:

search_space = ps(
  cost = p_dbl(-1, 1, trafo = function(x) 10^x),
  kernel = p_fct(c("polynomial", "radial")),
  degree = p_int(1, 3, depends = kernel == "polynomial")
)
rbindlist(generate_design_grid(search_space, 3)$transpose(), fill = TRUE)

##     cost     kernel degree
##  1:  0.1 polynomial      1
##  2:  0.1 polynomial      2
##  3:  0.1 polynomial      3
##  4:  0.1     radial     NA
##  5:  1.0 polynomial      1
##  6:  1.0 polynomial      2
##  7:  1.0 polynomial      3
##  8:  1.0     radial     NA
##  9: 10.0 polynomial      1
## 10: 10.0 polynomial      2
## 11: 10.0 polynomial      3
## 12: 10.0     radial     NA

Creating Tuning ParamSets from other ParamSets

Having to define a tuning ParamSet for a Learner that already has parameter set information may seem unnecessarily tedious, and there is indeed a way to create tuning ParamSets from a Learner’s ParamSet, making use of as much information as already available.

This is done by setting values of a Learner’s ParamSet to so-called TuneTokens, constructed with a to_tune call. This can be done in the same way that other hyperparameters are set to specific values. It can be understood as the hyperparameters being tagged for later tuning. The resulting ParamSet used for tuning can be retrieved using the $search_space() method.

library("mlr3learners")

## Loading required package: mlr3

learner = lrn("classif.svm")
learner$param_set$values$kernel = "polynomial" # for example
learner$param_set$values$degree = to_tune(lower = 1, upper = 3)

print(learner$param_set$search_space())

## <ParamSet>
##        id    class lower upper nlevels        default value
## 1: degree ParamInt     1     3       3 <NoDefault[3]>

rbindlist(generate_design_grid(
  learner$param_set$search_space(), 3)$transpose()
)

##    degree
## 1:      1
## 2:      2
## 3:      3

It is possible to omit lower here, because it can be inferred from the lower bound of the degree parameter itself. For other parameters, that are already bounded, it is possible to not give any bounds at all, because their ranges are already bounded. An example is the logical shrinking hyperparameter:

learner$param_set$values$shrinking = to_tune()

print(learner$param_set$search_space())

## <ParamSet>
##           id    class lower upper nlevels        default value
## 1:    degree ParamInt     1     3       3 <NoDefault[3]>      
## 2: shrinking ParamLgl    NA    NA       2           TRUE

rbindlist(generate_design_grid(
  learner$param_set$search_space(), 3)$transpose()
)

##    degree shrinking
## 1:      1      TRUE
## 2:      1     FALSE
## 3:      2      TRUE
## 4:      2     FALSE
## 5:      3      TRUE
## 6:      3     FALSE

"to_tune" can also be constructed with a Domain object, i.e. something constructed with a p_*** call. This way it is possible to tune continuous parameters with discrete values, or to give trafos or dependencies. One could, for example, tune the cost as above on three given special values, and introduce a dependency of shrinking on it. Notice that a short form for to_tune(<levels>) is a short form of to_tune(p_fct(<levels>)). When introducing the dependency, we need to use the degree value from before the implicit trafo, which is the name or as.character() of the respective value, here "val2"!

learner$param_set$values$type = "C-classification" # needs to be set because of a bug in paradox
learner$param_set$values$cost = to_tune(c(val1 = 0.3, val2 = 0.7))
learner$param_set$values$shrinking = to_tune(p_lgl(depends = cost == "val2"))

print(learner$param_set$search_space())

## <ParamSet>
##           id    class lower upper nlevels        default parents value
## 1:      cost ParamFct    NA    NA       2 <NoDefault[3]>              
## 2:    degree ParamInt     1     3       3 <NoDefault[3]>              
## 3: shrinking ParamLgl    NA    NA       2 <NoDefault[3]>    cost      
## Trafo is set.

rbindlist(generate_design_grid(learner$param_set$search_space(), 3)$transpose(), fill = TRUE)

##    degree cost shrinking
## 1:      1  0.3        NA
## 2:      1  0.7      TRUE
## 3:      1  0.7     FALSE
## 4:      2  0.3        NA
## 5:      2  0.7      TRUE
## 6:      2  0.7     FALSE
## 7:      3  0.3        NA
## 8:      3  0.7      TRUE
## 9:      3  0.7     FALSE

The search_space() picks up dependencies from the underlying ParamSet automatically. So if the kernel is tuned, then degree automatically gets the dependency on it, without us having to specify that. (Here we reset cost and shrinking to NULL for the sake of clarity of the generated output.)

learner$param_set$values$cost = NULL
learner$param_set$values$shrinking = NULL
learner$param_set$values$kernel = to_tune(c("polynomial", "radial"))

print(learner$param_set$search_space())

## <ParamSet>
##        id    class lower upper nlevels        default parents value
## 1: degree ParamInt     1     3       3 <NoDefault[3]>  kernel      
## 2: kernel ParamFct    NA    NA       2 <NoDefault[3]>

rbindlist(generate_design_grid(learner$param_set$search_space(), 3)$transpose(), fill = TRUE)

##        kernel degree
## 1: polynomial      1
## 2: polynomial      2
## 3: polynomial      3
## 4:     radial     NA

It is even possible to define whole ParamSets that get tuned over for a single parameter. This may be especially useful for vector hyperparameters that should be searched along multiple dimensions. This ParamSet must, however, have an .extra_trafo that returns a list with a single element, because it corresponds to a single hyperparameter that is being tuned. Suppose the class.weights hyperparameter should be tuned along two dimensions:

learner$param_set$values$class.weights = to_tune(
  ps(spam = p_dbl(0.1, 0.9), nonspam = p_dbl(0.1, 0.9),
    .extra_trafo = function(x, param_set) list(c(spam = x$spam, nonspam = x$nonspam))
))
head(generate_design_grid(learner$param_set$search_space(), 3)$transpose(), 3)

## [[1]]
## [[1]]$kernel
## [1] "polynomial"
## 
## [[1]]$degree
## [1] 1
## 
## [[1]]$class.weights
##    spam nonspam 
##     0.1     0.1 
## 
## 
## [[2]]
## [[2]]$kernel
## [1] "polynomial"
## 
## [[2]]$degree
## [1] 1
## 
## [[2]]$class.weights
##    spam nonspam 
##     0.1     0.5 
## 
## 
## [[3]]
## [[3]]$kernel
## [1] "polynomial"
## 
## [[3]]$degree
## [1] 1
## 
## [[3]]$class.weights
##    spam nonspam 
##     0.1     0.9

Parameters (using paradox)

Reference Based Objects

Defining a Parameter Space

Single Parameters

Type / Range Checking

Parameter Sets

Type / Range Checking

Values in a ParamSet

Dependencies

Vector Parameters

Parameter Sampling

Parameter Designs

Grid Design

Random Sampling

Generalized Sampling: The Sampler Class

1D-Samplers

Hierarchical Sampler

Joint Sampler

SamplerUnif

Parameter Transformation

Transformation between Types

Defining a Tuning Spaces

Creating ParamSets

Transformations (trafo)

Automatic Factor Level Transformation

Parameter Dependencies (depends)

Creating Tuning ParamSets from other ParamSets

Values in a `ParamSet`

Generalized Sampling: The `Sampler` Class

Creating `ParamSet`s

Transformations (`trafo`)

Parameter Dependencies (`depends`)