Parameters (using paradox)
The paradox package offers a language for the
description of parameter spaces, as well as tools for useful
operations on these parameter spaces. A parameter space is often useful
when describing:
- A set of sensible input values for an R function
- The set of possible values that slots of a configuration object can take
- The search space of an optimization process
The tools provided by paradox therefore relate to:
- Parameter checking: Verifying that a set of parameters satisfies the conditions of a parameter space
- Parameter sampling: Generating parameter values that lie in the parameter space for systematic exploration of program behavior depending on these parameters
paradox is, by nature, an auxiliary package that derives
its usefulness from other packages that make use of it. It is heavily
utilized in other mlr-org
packages such as mlr3, mlr3pipelines,
mlr3tuning and miesmuschel.
Reference Based Objects
paradox is the spiritual successor to the
ParamHelpers package and was written from scratch. The most
important consequence of this is that some objects created in
paradox are “reference-based”, unlike most other objects in
R. When a change is made to a ParamSet object, for example
by changing the $values field, all variables that point to
this ParamSet will contain the changed object. To create an
independent copy of a ParamSet, the
$clone(deep = TRUE) method needs to be used:
library("paradox")
ps1 = ps(a = p_int(init = 1))
ps2 = ps1
ps3 = ps1$clone(deep = TRUE)
print(ps1) # the same for ps2 and ps3
#> <ParamSet(1)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: a ParamInt -Inf Inf Inf <NoDefault[0]> 1
ps1$values$a = 2
print(ps1) # ps1 value of 'a' was changed
#> <ParamSet(1)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: a ParamInt -Inf Inf Inf <NoDefault[0]> 2
print(ps2) # contains the same reference as ps1, so also changed
#> <ParamSet(1)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: a ParamInt -Inf Inf Inf <NoDefault[0]> 2
print(ps3) # is a "clone" of the old ps1 with 'a' == 1
#> <ParamSet(1)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: a ParamInt -Inf Inf Inf <NoDefault[0]> 1Defining a Parameter Space
Domain Representing Single Parameters
Parameter spaces are made up of individual parameters, which usually
can take a single atomic value. Consider, for example, trying to
configure the rpart package’s rpart.control
object. It has various components (minsplit,
cp, …) that all take a single value.
These components are represented by Domain objects,
which are constructed by calls of the form p_xxx():
-
p_int()for integer numbers -
p_dbl()for real numbers -
p_fct()for categorical values, similar to Rfactors -
p_lgl()for truth values (TRUE/FALSE), aslogicals in R -
p_uty()for parameters that can take any value
A ParamSet that represent a given set of parameters is
created by calling ps() with named arguments that are
Domain objects. While Domain themselves are R
objects that can in principle be handled and manipulated, they should
not be changed after construction.
library("paradox")
param_set = ps(
parA = p_lgl(init = FALSE),
parB = p_int(lower = 0, upper = 10, tags = c("tag1", "tag2")),
parC = p_dbl(lower = 0, upper = 4, special_vals = list(NULL)),
parD = p_fct(levels = c("x", "y", "z"), default = "y"),
parE = p_uty(custom_check = function(x) checkmate::checkFunction(x))
)
param_set
#> <ParamSet(5)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: parA ParamLgl NA NA 2 <NoDefault[0]> FALSE
#> 2: parB ParamInt 0 10 11 <NoDefault[0]>
#> 3: parC ParamDbl 0 4 Inf <NoDefault[0]>
#> 4: parD ParamFct NA NA 3 y
#> 5: parE ParamUty NA NA Inf <NoDefault[0]>Every parameter can have:
- default - A default value, indicating the behaviour of something if the specific value is not given.
-
init - An initial value, which is set in
$valueswhen theParamSetis created. Note that this is not the same asdefault:defaultis used when a parameter is not present in$values, whileinitis the value that is set upon creation. - special_vals - A list of values that are accepted even if they do not conform to the type
- tags - Tags that can be used to organize parameters
-
trafo - A transformation function that is applied
to the parameter value after it has been sampled. It is for example used
through the
Design$transpose()function after aDesignwas created bygenerate_design_random()or similar functions.
The numeric (p_int() and p_dbl())
parameters furthermore allow for specification of a
lower and upper bound. Meanwhile, the
p_fct() parameter must be given a vector of
levels that define the possible states its parameter
can take. The p_uty parameter can also have a
custom_check function that must return
TRUE when a value is acceptable and may return a
character(1) error description otherwise. The example above
defines parE as a parameter that only accepts
functions.
All values which are given to the constructor are then accessible
from the ParamSet for inspection using $. The
ParamSet should be considered immutable, except for some
fields such as $values, $deps,
$tags. Bounds and levels should not be changed after
construction. Instead, a new ParamSet should be
constructed.
Besides the possible values that can be given to a constructor, there
are also the $class, $nlevels,
$is_bounded, $has_default,
$storage_type, $is_number and
$is_categ slots that give information about a
parameter.
A list of all slots can be found in ?Param.
param_set$lower
#> parA parB parC parD parE
#> NA 0 0 NA NA
param_set$parD$levels
#> NULL
param_set$class
#> parA parB parC parD parE
#> "ParamLgl" "ParamInt" "ParamDbl" "ParamFct" "ParamUty"It is also possible to get all information of a ParamSet
as data.table by calling as.data.table().
as.data.table(param_set)
#> id class lower upper levels nlevels is_bounded special_vals
#> <char> <char> <num> <num> <list> <num> <lgcl> <list>
#> 1: parA ParamLgl NA NA TRUE,FALSE 2 TRUE <list[0]>
#> 2: parB ParamInt 0 10 11 TRUE <list[0]>
#> 3: parC ParamDbl 0 4 Inf TRUE <list[1]>
#> 4: parD ParamFct NA NA x,y,z 3 TRUE <list[0]>
#> 5: parE ParamUty NA NA Inf FALSE <list[0]>
#> default storage_type tags
#> <list> <char> <list>
#> 1: <NoDefault[0]> logical
#> 2: <NoDefault[0]> integer tag1,tag2
#> 3: <NoDefault[0]> numeric
#> 4: y character
#> 5: <NoDefault[0]> listType / Range Checking
The ParamSet object offers the possibility to check
whether a value satisfies its condition, i.e. is of the right type, and
also falls within the range of allowed values, using the
$test(), $check(), and $assert()
functions. Their argument must be a named list with values that are
checked against the respective parameters, and it is possible to check
only a subset of parameters. test() should be used within
conditional checks and returns TRUE or FALSE,
while check() returns an error description when a value
does not conform to the parameter (and thus plays well with the
"checkmate::assert()" function). assert() will
throw an error whenever a value does not fit.
Parameter Sets
The ordered collection of parameters is handled in a
ParamSet. It is typically created by calling
ps(), but can also be initialized using the
ParamSet$new() function. The main difference is that
ps() takes named arguments, whereas
ParamSet$new() takes a named list. The latter makes it
easier to construct a ParamSet programmatically, but is
slightly more verbose.
ParamSets can be combined using c() or
ps_union (the latter of which takes a list), and they have
a $subset() method that allows for subsetting. All of these
functions return a new, cloned ParamSet object, and do not
modify the original ParamSet.
ps1 = ParamSet$new(list(x = p_int(), y = p_dbl()))
ps2 = ParamSet$new(list(z = p_fct(levels = c("a", "b", "c"))))
ps_all = c(ps1, ps2)
print(ps_all)
#> <ParamSet(3)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: x ParamInt -Inf Inf Inf <NoDefault[0]>
#> 2: y ParamDbl -Inf Inf Inf <NoDefault[0]>
#> 3: z ParamFct NA NA 3 <NoDefault[0]>
ps_all$subset(c("x", "z"))
#> <ParamSet(2)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: x ParamInt -Inf Inf Inf <NoDefault[0]>
#> 2: z ParamFct NA NA 3 <NoDefault[0]>ParamSets of each individual parameters can be accessed
through the $subspaces() function.
It is possible to get the ParamSet as a
data.table using as.data.table(). This makes
it easy to subset parameters on certain conditions and aggregate
information about them, using the variety of methods provided by
data.table.
as.data.table(ps_all)
#> id class lower upper levels nlevels is_bounded special_vals
#> <char> <char> <num> <num> <list> <num> <lgcl> <list>
#> 1: x ParamInt -Inf Inf Inf FALSE <list[0]>
#> 2: y ParamDbl -Inf Inf Inf FALSE <list[0]>
#> 3: z ParamFct NA NA a,b,c 3 TRUE <list[0]>
#> default storage_type tags
#> <list> <char> <list>
#> 1: <NoDefault[0]> integer
#> 2: <NoDefault[0]> numeric
#> 3: <NoDefault[0]> characterValues in a ParamSet
Although a ParamSet fundamentally represents a value
space, it also has a slot $values that can contain a point
within that space. This is useful because many things that define a
parameter space need similar operations (like parameter checking) that
can be simplified. The $values slot contains a named list
that is always checked against parameter constraints. When trying to set
parameter values, e.g. for mlr3 Learners, it
is the $values slot of its $param_set that
needs to be used.
ps1$values = list(x = 1, y = 1.5)
ps1$values$y = 2.5
print(ps1$values)
#> $x
#> [1] 1
#>
#> $y
#> [1] 2.5The parameter constraints are automatically checked:
ps1$values$x = 1.5
#> Error in self$assert(xs, sanitize = TRUE): Assertion on 'xs' failed: x: Must be of type 'single integerish value', not 'double'.Dependencies
It is often the case that certain parameters are irrelevant or should
not be given depending on values of other parameters. An example would
be a parameter that switches a certain algorithm feature (for example
regularization) on or off, combined with another parameter that controls
the behavior of that feature (e.g. a regularization parameter). The
second parameter would be said to depend on the first parameter
having the value TRUE.
A dependency can be added using the $add_dep method,
which takes both the ids of the “depender” and “dependee” parameters as
well as a Condition object. The Condition
object represents the check to be performed on the “dependee”. Currently
it can be created using CondEqual() and
CondAnyOf(). Multiple dependencies can be added, and
parameters that depend on others can again be depended on, as long as no
cyclic dependencies are introduced.
The consequence of dependencies are twofold: For one, the
$check(), $test() and $assert()
tests will not accept the presence of a parameter if its dependency is
not met, when the check_strict argument is given as
TRUE. Furthermore, when sampling or creating grid designs
from a ParamSet, the dependencies will be respected.
The easiest way to set dependencies is to give the
depends argument to the Domain
constructor.
The following example makes parameter D depend on
parameter A being FALSE, and parameter
B depend on parameter D being one of
"x" or "y". This introduces an implicit
dependency of B on A being FALSE
as well, because D does not take any value if
A is TRUE.
p = ps(
A = p_lgl(init = FALSE),
B = p_int(lower = 0, upper = 10, depends = D %in% c("x", "y")),
C = p_dbl(lower = 0, upper = 4),
D = p_fct(levels = c("x", "y", "z"), depends = A == FALSE)
)Note that the depends argument is limited to operators
== and %in%, so
D = p_fct(..., depends = !A) would not work.
p$check(list(A = FALSE, D = "x", B = 1), check_strict = TRUE) # OK: all dependencies met
#> [1] TRUE
p$check(list(A = FALSE, D = "z", B = 1), check_strict = TRUE) # B's dependency is not met
#> [1] "B: can only be set if the following condition is met 'D %in% {x, y}'. Instead the current parameter value is: D == z"
p$check(list(A = FALSE, B = 1), check_strict = TRUE) # B's dependency is not met
#> [1] "B: can only be set if the following condition is met 'D %in% {x, y}'. Instead the parameter value for 'D' is not set at all. Try setting 'D' to a value that satisfies the condition"
p$check(list(A = FALSE, D = "z"), check_strict = TRUE) # OK: B is absent
#> [1] TRUE
p$check(list(A = TRUE), check_strict = TRUE) # OK: neither B nor D present
#> [1] TRUE
p$check(list(A = TRUE, D = "x", B = 1), check_strict = TRUE) # D's dependency is not met
#> [1] "D: can only be set if the following condition is met 'A == FALSE'. Instead the current parameter value is: A == TRUE"
p$check(list(A = TRUE, B = 1), check_strict = TRUE) # B's dependency is not met
#> [1] "B: can only be set if the following condition is met 'D %in% {x, y}'. Instead the parameter value for 'D' is not set at all. Try setting 'D' to a value that satisfies the condition"Internally, the dependencies are represented as a
data.table, which can be accessed listed in the
$deps slot. This data.table
can even be mutated, to e.g. remove dependencies. There are no sanity
checks done when the $deps slot is changed this way.
Therefore it is advised to be cautious.
p$deps
#> Index: <id>
#> id on cond
#> <char> <char> <list>
#> 1: B D <Condition:CondAnyOf>
#> 2: D A <Condition:CondEqual>Vector Parameters
Unlike in the old ParamHelpers package, there are no
more vectorial parameters in paradox. Instead, it is now
possible to create multiple copies of a single parameter using the
ps_replicate function. This creates a ParamSet
consisting of multiple copies of the parameter, which can then
(optionally) be added to another ParamSet.
ps2d = ps_replicate(ps(x = p_dbl(lower = 0, upper = 1)), 2)
print(ps2d)
#> <ParamSet(2)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: rep1.x ParamDbl 0 1 Inf <NoDefault[0]>
#> 2: rep2.x ParamDbl 0 1 Inf <NoDefault[0]>It is also possible to use a ParamUty to accept
vectorial parameters, which also works for parameters of variable
length. A ParamSet containing a ParamUty can
be used for parameter checking, but not for sampling. To sample values
for a method that needs a vectorial parameter, it is advised to use an
$extra_trafo transformation function that creates a vector
from atomic values.
Assembling a vector from repeated parameters is aided by the
parameter’s $tags: Parameters that were generated by the
pr_replicate() command can be tagged as belonging to a
group of repeated parameters.
ps2d = ps_replicate(ps(x = p_dbl(0, 1), y = p_int(0, 10)), 2, tag_params = TRUE)
ps2d$values = list(rep1.x = 0.2, rep2.x = 0.4, rep1.y = 3, rep2.y = 4)
ps2d$tags
#> $rep1.x
#> [1] "param_x"
#>
#> $rep1.y
#> [1] "param_y"
#>
#> $rep2.x
#> [1] "param_x"
#>
#> $rep2.y
#> [1] "param_y"
ps2d$get_values(tags = "param_x")
#> $rep1.x
#> [1] 0.2
#>
#> $rep2.x
#> [1] 0.4Parameter Sampling
It is often useful to have a list of possible parameter values that
can be systematically iterated through, for example to find parameter
values for which an algorithm performs particularly well (tuning).
paradox offers a variety of functions that allow creating
evenly-spaced parameter values in a “grid” design as well as random
sampling. In the latter case, it is possible to influence the sampling
distribution in more or less fine detail.
A point to always keep in mind while sampling is that only numerical
and factorial parameters that are bounded can be sampled from, i.e. not
ParamUty. Furthermore, for most samplers
p_int() and p_dbl() must have finite lower and
upper bounds.
Parameter Designs
Functions that sample the parameter space fundamentally return an
object of the Design class. These objects contain the
sampled data as a data.table under the $data
slot, and also offer conversion to a list of parameter-values using the
$transpose() function.
Grid Design
The generate_design_grid() function is used to create
grid designs that contain all combinations of parameter values: All
possible values for ParamLgl and ParamFct, and
values with a given resolution for ParamInt and
ParamDbl. The resolution can be given for all numeric
parameters, or for specific named parameters through the
param_resolutions parameter.
ps_small = ps(A = p_dbl(0, 1), B = p_dbl(0, 1))
design = generate_design_grid(ps_small, 2)
print(design)
#> <Design> with 4 rows:
#> A B
#> <num> <num>
#> 1: 0 0
#> 2: 0 1
#> 3: 1 0
#> 4: 1 1
generate_design_grid(ps_small, param_resolutions = c(A = 3, B = 2))
#> <Design> with 6 rows:
#> A B
#> <num> <num>
#> 1: 0.0 0
#> 2: 0.0 1
#> 3: 0.5 0
#> 4: 0.5 1
#> 5: 1.0 0
#> 6: 1.0 1Random Sampling
paradox offers different methods for random sampling,
which vary in the degree to which they can be configured. The easiest
way to get a uniformly random sample of parameters is
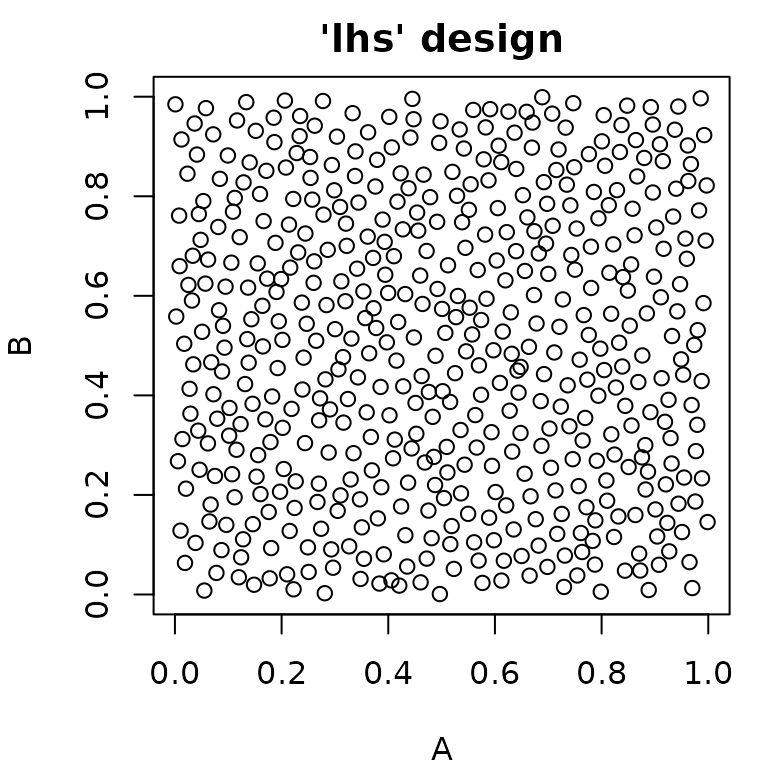
generate_design_random(). It is also possible to create “latin
hypercube” sampled parameter values using
generate_design_lhs(), which utilizes the lhs
package. LHS-sampling creates low-discrepancy sampled values that cover
the parameter space more evenly than purely random values.
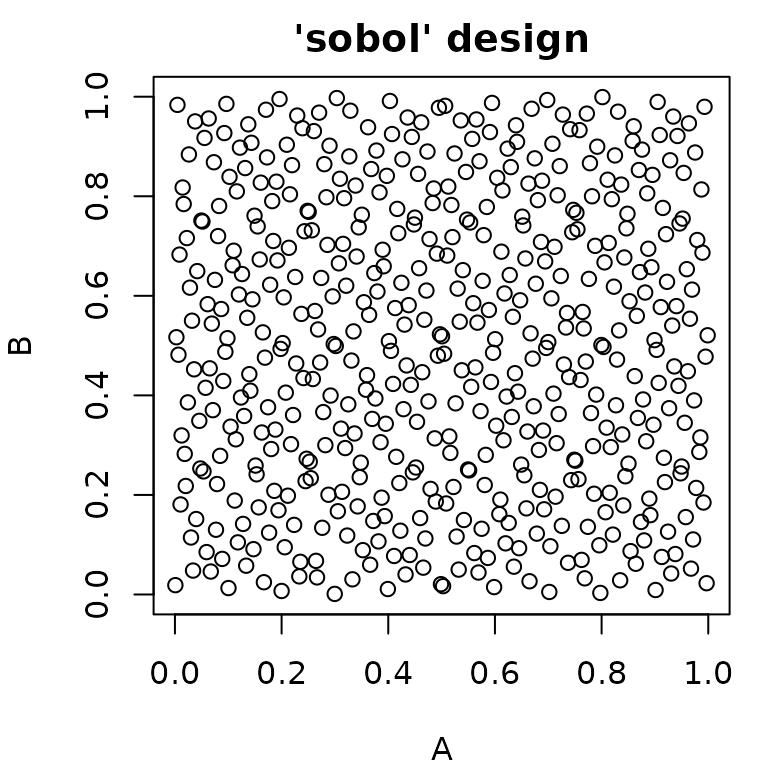
generate_design_sobol() can be used to sample using the Sobol
sequence.
pvrand = generate_design_random(ps_small, 500)
pvlhs = generate_design_lhs(ps_small, 500)
pvsobol = generate_design_sobol(ps_small, 500)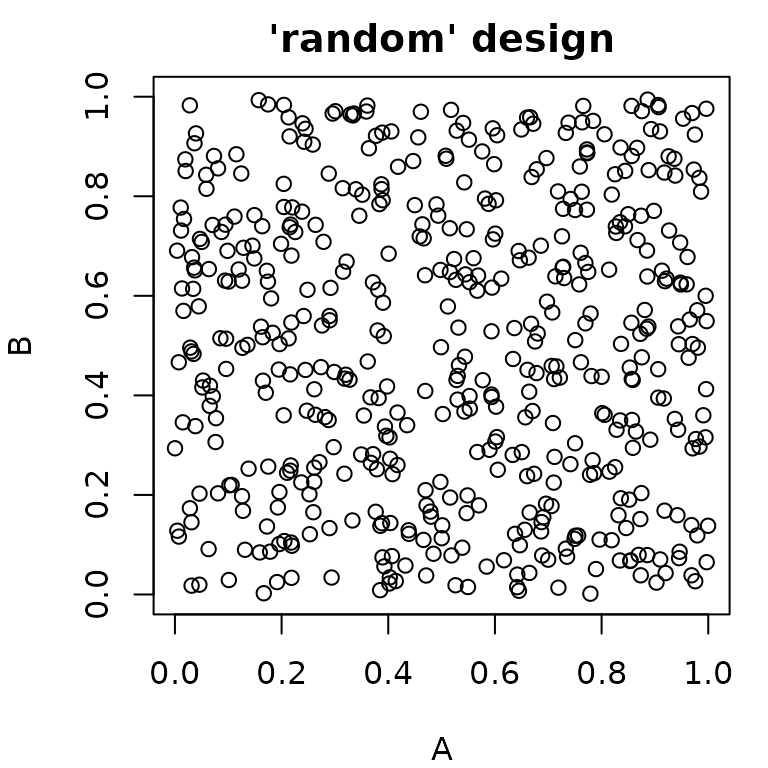
Generalized Sampling: The Sampler Class
It may sometimes be desirable to configure parameter sampling in more
detail. paradox uses the Sampler abstract base
class for sampling, which has many different sub-classes that can be
parameterized and combined to control the sampling process. It is even
possible to create further sub-classes of the Sampler class
(or of any of its subclasses) for even more possibilities.
Every Sampler object has a sample()
function, which takes one argument, the number of instances to sample,
and returns a Design object.
1D-Samplers
There is a variety of samplers that sample values for a single
parameter. These are Sampler1DUnif (uniform sampling),
Sampler1DCateg (sampling for categorical parameters),
Sampler1DNormal (normally distributed sampling, truncated
at parameter bounds), and Sampler1DRfun (arbitrary 1D
sampling, given a random-function). These are initialized with a
one-dimensional ParamSet, and can then be used to sample
values.
sampA = Sampler1DCateg$new(ps(x = p_fct(letters)))
sampA$sample(5)
#> <Design> with 5 rows:
#> x
#> <char>
#> 1: f
#> 2: k
#> 3: e
#> 4: g
#> 5: fHierarchical Sampler
The SamplerHierarchical sampler is an auxiliary sampler
that combines many 1D-Samplers to get a combined distribution. Its name
“hierarchical” implies that it is able to respect parameter
dependencies. This suggests that parameters only get sampled when their
dependencies are met.
The following example shows how this works: The Int
parameter B depends on the Lgl parameter
A being TRUE. A is sampled to be
TRUE in about half the cases, in which case B
takes a value between 0 and 10. In the cases where A is
FALSE, B is set to NA.
p = ps(
A = p_lgl(),
B = p_int(0, 10, depends = A == TRUE)
)
p_subspaces = p$subspaces()
sampH = SamplerHierarchical$new(p,
list(Sampler1DCateg$new(p_subspaces$A),
Sampler1DUnif$new(p_subspaces$B))
)
sampled = sampH$sample(1000)
head(sampled$data)
#> A B
#> <lgcl> <int>
#> 1: FALSE NA
#> 2: FALSE NA
#> 3: TRUE 7
#> 4: TRUE 10
#> 5: TRUE 2
#> 6: FALSE NA
table(sampled$data[, c("A", "B")], useNA = "ifany")
#> B
#> A 0 1 2 3 4 5 6 7 8 9 10 <NA>
#> FALSE 0 0 0 0 0 0 0 0 0 0 0 492
#> TRUE 50 45 57 49 49 38 39 47 44 42 48 0Joint Sampler
Another way of combining samplers is the
SamplerJointIndep. SamplerJointIndep also
makes it possible to combine Samplers that are not 1D.
However, SamplerJointIndep currently can not handle
ParamSets with dependencies.
sampJ = SamplerJointIndep$new(
list(Sampler1DUnif$new(ps(x = p_dbl(0, 1))),
Sampler1DUnif$new(ps(y = p_dbl(0, 1))))
)
sampJ$sample(5)
#> <Design> with 5 rows:
#> x y
#> <num> <num>
#> 1: 0.4889776 0.454001049
#> 2: 0.2828764 0.165267821
#> 3: 0.8167114 0.959529563
#> 4: 0.9697799 0.003741143
#> 5: 0.2319606 0.646213624SamplerUnif
The Sampler used in
generate_design_random() is the SamplerUnif
sampler, which corresponds to a HierarchicalSampler of
Sampler1DUnif for all parameters.
Parameter Transformation
While the different Samplers allow for a wide
specification of parameter distributions, there are cases where the
simplest way of getting a desired distribution is to sample parameters
from a simple distribution (such as the uniform distribution) and then
transform them. This can be done by constructing a Domain
with a trafo argument, or assigning a function to the
$extra_trafo field of a ParamSet. The latter
can also be done by passing an .extra_trafo argument to the
ps() shorthand constructor.
A trafo function in a Domain is called with
a single parameter, the value to be transformed. It can only operate on
the dimension of a single parameter.
The $extra_trafo function is called with two
parameters:
- The list of parameter values to be transformed as
x. Unlike theDomain’strafo, the$extra_trafohandles the whole parameter set and can even model “interactions” between parameters. - The
ParamSetitself asparam_set
The $extra_trafo function must return a list of
transformed parameter values.
The transformation is performed when calling the
$transpose function of the Design object
returned by a Sampler with the trafo ParamSet
to TRUE (the default). The following, for example, creates
a parameter that is exponentially distributed:
psexp = ps(par = p_dbl(0, 1, trafo = function(x) -log(x)))
design = generate_design_random(psexp, 3)
print(design) # not transformed: between 0 and 1
#> <Design> with 3 rows:
#> par
#> <num>
#> 1: 0.9824873
#> 2: 0.4098267
#> 3: 0.7395942
design$transpose() # trafo is TRUE
#> [[1]]
#> [[1]]$par
#> [1] 0.01766784
#>
#>
#> [[2]]
#> [[2]]$par
#> [1] 0.892021
#>
#>
#> [[3]]
#> [[3]]$par
#> [1] 0.3016537Compare this to $transpose() without transformation:
design$transpose(trafo = FALSE)
#> [[1]]
#> [[1]]$par
#> [1] 0.9824873
#>
#>
#> [[2]]
#> [[2]]$par
#> [1] 0.4098267
#>
#>
#> [[3]]
#> [[3]]$par
#> [1] 0.7395942Another way to get tihs effect, using $extra_trafo,
would be:
However, the trafo way is more recommended when
transforming parameters independently. $extra_trafo is more
useful when transforming parameters that interact in some way, or when
new parameters should be generated.
Transformation between Types
Usually the design created with one ParamSet is then
used to configure other objects that themselves have a
ParamSet which defines the values they take. The
ParamSets which can be used for random sampling, however,
are restricted in some ways: They must have finite bounds, and they may
not contain “untyped” (ParamUty) parameters.
$trafo provides the glue for these situations. There is
relatively little constraint on the trafo function’s return value, so it
is possible to return values that have different bounds or even types
than the original ParamSet. It is even possible to remove
some parameters and add new ones.
Suppose, for example, that a certain method requires a
function as a parameter. Let’s say a function that summarizes
its data in a certain way. The user can pass functions like
median() or mean(), but could also pass
quantiles or something completely different. This method would probably
use the following ParamSet:
methodPS = ps(fun = p_uty(custom_check = function(x) checkmate::checkFunction(x, nargs = 1)))
print(methodPS)
#> <ParamSet(1)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: fun ParamUty NA NA Inf <NoDefault[0]>If one wanted to sample this method, using one of four functions, a way to do this would be:
samplingPS = ps(
fun = p_fct(c("mean", "median", "min", "max"),
trafo = function(x) get(x, mode = "function"))
)
design = generate_design_random(samplingPS, 2)
print(design)
#> <Design> with 2 rows:
#> fun
#> <char>
#> 1: min
#> 2: medianNote that the Design only contains the column
“fun” as a character column. To get a single
value as a function, the $transpose function is
used.
xvals = design$transpose()
print(xvals[[1]])
#> $fun
#> function (..., na.rm = FALSE) .Primitive("min")We can now check that it fits the requirements set by
methodPS, and that fun it is in fact a
function:
methodPS$check(xvals[[1]])
#> [1] TRUE
xvals[[1]]$fun(1:10)
#> [1] 1p_fct() has a shortcut for this kind of transformation,
where a character is transformed into a specific set of
(typically non-scalar) values. When its levels argument is
given as a named list (or named non-character
vector), it constructs a Domain that does the trafo
automatically. A way to perform the above would therefore be:
samplingPS = ps(
fun = p_fct(list("mean" = mean, "median" = median, "min" = min, "max" = max))
)
generate_design_random(samplingPS, 1)$transpose()
#> [[1]]
#> [[1]]$fun
#> function (x, ...)
#> UseMethod("mean")
#> <bytecode: 0x55c8a1c80a90>
#> <environment: namespace:base>Imagine now that a different kind of parametrization of the function
is desired: The user wants to give a function that selects a certain
quantile, where the quantile is set by a parameter. In that case the
$transpose function could generate a function in a
different way.
For interpretability, the parameter should be called
“quantile” before transformation, and the
“fun” parameter is generated on the fly. We therefore use
an extra_trafo here, given as a function to the
ps() call.
samplingPS2 = ps(quantile = p_dbl(0, 1),
.extra_trafo = function(x, param_set) {
# x$quantile is a `numeric(1)` between 0 and 1.
# We want to turn it into a function!
list(fun = function(input) quantile(input, x$quantile))
}
)
design = generate_design_random(samplingPS2, 2)
print(design)
#> <Design> with 2 rows:
#> quantile
#> <num>
#> 1: 0.6744397
#> 2: 0.9373676The Design now contains the column
“quantile” that will be used by the $transpose
function to create the fun parameter. We also check that it
fits the requirement set by methodPS, and that it is a
function.
xvals = design$transpose()
print(xvals[[1]])
#> $fun
#> function(input) quantile(input, x$quantile)
#> <environment: 0x55c8a5112b78>
methodPS$check(xvals[[1]])
#> [1] TRUE
xvals[[1]]$fun(1:10)
#> 67.44397%
#> 7.069958Defining a Tuning Spaces
When running an optimization, it is important to inform the tuning
algorithm about what hyperparameters are valid. Here the names, types,
and valid ranges of each hyperparameter are important. All this
information is communicated with objects of the class
ParamSet, which is defined in paradox.
Note, that ParamSet objects exist in two contexts.
First, ParamSet-objects are used to define the space of
valid parameter settings for a learner (and other objects). Second, they
are used to define a search space for tuning. We are mainly interested
in the latter. For example we can consider the minsplit
parameter of the
mlr_learners_classif.rpart", "classif.rpart Learner. The
ParamSet associated with the learner has a lower but
no upper bound. However, for tuning the value, a lower
and upper bound must be given because tuning search spaces need
to be bounded. For Learner or PipeOp objects,
typically “unbounded” ParamSets are used. Here, however, we
will mainly focus on creating “bounded” ParamSets that can
be used for tuning.
Creating ParamSets
An empty "ParamSet – not yet very useful – can be
constructed using just the "ps" call:
ps takes named Domain arguments that are
turned into parameters. A possible search space for the
"classif.svm" learner could for example be:
search_space = ps(
cost = p_dbl(lower = 0.1, upper = 10),
kernel = p_fct(levels = c("polynomial", "radial"))
)
print(search_space)
#> <ParamSet(2)>
#> id class lower upper nlevels default value
#> <char> <char> <num> <num> <num> <list> <list>
#> 1: cost ParamDbl 0.1 10 Inf <NoDefault[0]>
#> 2: kernel ParamFct NA NA 2 <NoDefault[0]>There are five domain constructors that produce a parameters when
given to ps:
| Constructor | Description | Is bounded? |
|---|---|---|
p_dbl |
Real valued parameter (“double”) | When upper and lower are
given |
p_int |
Integer parameter | When upper and lower are
given |
p_fct |
Discrete valued parameter (“factor”) | Always |
p_lgl |
Logical / Boolean parameter | Always |
p_uty |
Untyped parameter | Never |
These domain constructors each take some of the following arguments:
-
lower,upper: lower and upper bound of numerical parameters (p_dblandp_int). These need to be given to get bounded parameter spaces valid for tuning. -
levels: Allowed categorical values forp_fctparameters. Required argument forp_fct. See below for more details on this parameter. -
trafo: transformation function, see below. -
depends: dependencies, see below. -
tags: Further information about a parameter, used for example by thehyperbandtuner. -
init: . Not used for tuning search spaces. -
default: Value corresponding to default behavior when the parameter is not given. Not used for tuning search spaces. -
special_vals: Valid values besides the normally accepted values for a parameter. Not used for tuning search spaces. -
custom_check: Function that checks whether a value given top_utyis valid. Not used for tuning search spaces.
The lower and upper parameters are always
in the first and second position respectively, except for
p_fct where levels is in the first position.
It is preferred to omit the labels (ex: upper = 0.1 becomes
just 0.1). This way of defining a ParamSet is
more concise than the equivalent definition above. Preferred:
Transformations (trafo)
We can use the paradox function
generate_design_grid to look at the values that would be
evaluated by grid search. (We are using rbindlist() here
because the result of $transpose() is a list that is harder
to read. If we didn’t use $transpose(), on the other hand,
the transformations that we investigate here are not applied.) In
generate_design_grid(search_space, 3),
search_space is the ParamSet argument and 3 is
the specified resolution in the parameter space. The resolution for
categorical parameters is ignored; these parameters always produce a
grid over all of their valid levels. For numerical parameters the
endpoints of the params are always included in the grid, so if there
were 3 levels for the kernel instead of 2 there would be 9 rows, or if
the resolution was 4 in this example there would be 8 rows in the
resulting table.
library("data.table")
rbindlist(generate_design_grid(search_space, 3)$transpose())
#> cost kernel
#> <num> <char>
#> 1: 0.10 polynomial
#> 2: 0.10 radial
#> 3: 5.05 polynomial
#> 4: 5.05 radial
#> 5: 10.00 polynomial
#> 6: 10.00 radialWe notice that the cost parameter is taken on a linear
scale. We assume, however, that the difference of cost between
0.1 and 1 should have a similar effect as the
difference between 1 and 10. Therefore it
makes more sense to tune it on a logarithmic scale. This is
done by using a transformation (trafo).
This is a function that is applied to a parameter after it has been
sampled by the tuner. We can tune cost on a logarithmic
scale by sampling on the linear scale [-1, 1] and computing
10^x from that value.
search_space = ps(
cost = p_dbl(-1, 1, trafo = function(x) 10^x),
kernel = p_fct(c("polynomial", "radial"))
)
rbindlist(generate_design_grid(search_space, 3)$transpose())
#> cost kernel
#> <num> <char>
#> 1: 0.1 polynomial
#> 2: 0.1 radial
#> 3: 1.0 polynomial
#> 4: 1.0 radial
#> 5: 10.0 polynomial
#> 6: 10.0 radialIt is even possible to attach another transformation to the
ParamSet as a whole that gets executed after individual
parameter’s transformations were performed. It is given through the
.extra_trafo argument and should be a function with
parameters x and param_set that takes a list
of parameter values in x and returns a modified list. This
transformation can access all parameter values of an evaluation and
modify them with interactions. It is even possible to add or remove
parameters. (The following is a bit of a silly example.)
search_space = ps(
cost = p_dbl(-1, 1, trafo = function(x) 10^x),
kernel = p_fct(c("polynomial", "radial")),
.extra_trafo = function(x, param_set) {
if (x$kernel == "polynomial") {
x$cost = x$cost * 2
}
x
}
)
rbindlist(generate_design_grid(search_space, 3)$transpose())
#> cost kernel
#> <num> <char>
#> 1: 0.2 polynomial
#> 2: 0.1 radial
#> 3: 2.0 polynomial
#> 4: 1.0 radial
#> 5: 20.0 polynomial
#> 6: 10.0 radialThe available types of search space parameters are limited:
continuous, integer, discrete, and logical scalars. There are many
machine learning algorithms, however, that take parameters of other
types, for example vectors or functions. These can not be defined in a
search space ParamSet, and they are often given as
p_uty() in the Learner’s
ParamSet. When trying to tune over these hyperparameters,
it is necessary to perform a Transformation that changes the type of a
parameter.
An example is the class.weights parameter of the Support
Vector Machine (SVM), which takes a named vector of class weights
with one entry for each target class. The trafo that would tune
class.weights for the tsk("spam") dataset
could be:
search_space = ps(
class.weights = p_dbl(0.1, 0.9, trafo = function(x) c(spam = x, nonspam = 1 - x))
)
generate_design_grid(search_space, 3)$transpose()
#> [[1]]
#> [[1]]$class.weights
#> spam nonspam
#> 0.1 0.9
#>
#>
#> [[2]]
#> [[2]]$class.weights
#> spam nonspam
#> 0.5 0.5
#>
#>
#> [[3]]
#> [[3]]$class.weights
#> spam nonspam
#> 0.9 0.1(We are omitting rbindlist() in this example because it
breaks the vector valued return elements.)
Automatic Factor Level Transformation
A common use-case is the necessity to specify a list of values that
should all be tried (or sampled from). It may be the case that a
hyperparameter accepts function objects as values and a certain list of
functions should be tried. Or it may be that a choice of special numeric
values should be tried. For this, the p_fct constructor’s
level argument may be a value that is not a
character vector, but something else. If, for example, only
the values 0.1, 3, and 10 should
be tried for the cost parameter, even when doing random
search, then the following search space would achieve that:
search_space = ps(
cost = p_fct(c(0.1, 3, 10)),
kernel = p_fct(c("polynomial", "radial"))
)
rbindlist(generate_design_grid(search_space, 3)$transpose())
#> cost kernel
#> <num> <char>
#> 1: 0.1 polynomial
#> 2: 0.1 radial
#> 3: 3.0 polynomial
#> 4: 3.0 radial
#> 5: 10.0 polynomial
#> 6: 10.0 radialThis is equivalent to the following:
search_space = ps(
cost = p_fct(c("0.1", "3", "10"),
trafo = function(x) list(`0.1` = 0.1, `3` = 3, `10` = 10)[[x]]),
kernel = p_fct(c("polynomial", "radial"))
)
rbindlist(generate_design_grid(search_space, 3)$transpose())
#> cost kernel
#> <num> <char>
#> 1: 0.1 polynomial
#> 2: 0.1 radial
#> 3: 3.0 polynomial
#> 4: 3.0 radial
#> 5: 10.0 polynomial
#> 6: 10.0 radialNote: Though the resolution is 3 here, in this case it doesn’t matter
because both cost and kernel are factors (the
resolution for categorical variables is ignored, these parameters always
produce a grid over all their valid levels).
This may seem silly, but makes sense when considering that factorial
tuning parameters are always character values:
search_space = ps(
cost = p_fct(c(0.1, 3, 10)),
kernel = p_fct(c("polynomial", "radial"))
)
typeof(search_space$params$cost$levels)
#> [1] "NULL"Be aware that this results in an “unordered” hyperparameter, however.
Tuning algorithms that make use of ordering information of parameters,
like genetic algorithms or model based optimization, will perform worse
when this is done. For these algorithms, it may make more sense to
define a p_dbl or p_int with a more fitting
trafo.
The class.weights case from above can also be
implemented like this, if there are only a few candidates of
class.weights vectors that should be tried. Note that the
levels argument of p_fct must be named if
there is no easy way for as.character() to create
names:
search_space = ps(
class.weights = p_fct(
list(
candidate_a = c(spam = 0.5, nonspam = 0.5),
candidate_b = c(spam = 0.3, nonspam = 0.7)
)
)
)
generate_design_grid(search_space)$transpose()
#> [[1]]
#> [[1]]$class.weights
#> spam nonspam
#> 0.5 0.5
#>
#>
#> [[2]]
#> [[2]]$class.weights
#> spam nonspam
#> 0.3 0.7Parameter Dependencies (depends)
Some parameters are only relevant when another parameter has a
certain value, or one of several values. The Support
Vector Machine (SVM), for example, has the degree
parameter that is only valid when kernel is
"polynomial". This can be specified using the
depends argument. It is an expression that must involve
other parameters and be of the form
<param> == <scalar>,
<param> %in% <vector>, or multiple of these
chained by &&. To tune the degree
parameter, one would need to do the following:
search_space = ps(
cost = p_dbl(-1, 1, trafo = function(x) 10^x),
kernel = p_fct(c("polynomial", "radial")),
degree = p_int(1, 3, depends = kernel == "polynomial")
)
rbindlist(generate_design_grid(search_space, 3)$transpose(), fill = TRUE)
#> cost kernel degree
#> <num> <char> <int>
#> 1: 0.1 polynomial 1
#> 2: 0.1 polynomial 2
#> 3: 0.1 polynomial 3
#> 4: 0.1 radial NA
#> 5: 1.0 polynomial 1
#> 6: 1.0 polynomial 2
#> 7: 1.0 polynomial 3
#> 8: 1.0 radial NA
#> 9: 10.0 polynomial 1
#> 10: 10.0 polynomial 2
#> 11: 10.0 polynomial 3
#> 12: 10.0 radial NACreating Tuning ParamSets from other ParamSets
Having to define a tuning ParamSet for a
Learner that already has parameter set information may seem
unnecessarily tedious, and there is indeed a way to create tuning
ParamSets from a Learner’s
ParamSet, making use of as much information as already
available.
This is done by setting values of a Learner’s
ParamSet to so-called TuneTokens, constructed
with a to_tune call. This can be done in the same way that
other hyperparameters are set to specific values. It can be understood
as the hyperparameters being tagged for later tuning. The resulting
ParamSet used for tuning can be retrieved using the
$search_space() method.
library("mlr3learners")
learner = lrn("classif.svm")
learner$param_set$values$kernel = "polynomial" # for example
learner$param_set$values$degree = to_tune(lower = 1, upper = 3)
print(learner$param_set$search_space())
rbindlist(generate_design_grid(
learner$param_set$search_space(), 3)$transpose()
)It is possible to omit lower here, because it can be
inferred from the lower bound of the degree parameter
itself. For other parameters, that are already bounded, it is possible
to not give any bounds at all, because their ranges are already bounded.
An example is the logical shrinking hyperparameter:
learner$param_set$values$shrinking = to_tune()
print(learner$param_set$search_space())
rbindlist(generate_design_grid(
learner$param_set$search_space(), 3)$transpose()
)"to_tune" can also be constructed with a
Domain object, i.e. something constructed with a
p_*** call. This way it is possible to tune continuous
parameters with discrete values, or to give trafos or dependencies. One
could, for example, tune the cost as above on three given
special values, and introduce a dependency of shrinking on
it. Notice that a short form for to_tune(<levels>) is
a short form of to_tune(p_fct(<levels>)). When
introducing the dependency, we need to use the degree value
from before the implicit trafo, which is the name or
as.character() of the respective value, here
"val2"!
learner$param_set$values$type = "C-classification" # needs to be set because of a bug in paradox
learner$param_set$values$cost = to_tune(c(val1 = 0.3, val2 = 0.7))
learner$param_set$values$shrinking = to_tune(p_lgl(depends = cost == "val2"))
print(learner$param_set$search_space())
rbindlist(generate_design_grid(learner$param_set$search_space(), 3)$transpose(), fill = TRUE)The search_space() picks up dependencies from the
underlying ParamSet automatically. So if the
kernel is tuned, then degree automatically
gets the dependency on it, without us having to specify that. (Here we
reset cost and shrinking to NULL
for the sake of clarity of the generated output.)
learner$param_set$values$cost = NULL
learner$param_set$values$shrinking = NULL
learner$param_set$values$kernel = to_tune(c("polynomial", "radial"))
print(learner$param_set$search_space())
rbindlist(generate_design_grid(learner$param_set$search_space(), 3)$transpose(), fill = TRUE)It is even possible to define whole ParamSets that get
tuned over for a single parameter. This may be especially useful for
vector hyperparameters that should be searched along multiple
dimensions. This ParamSet must, however, have an
.extra_trafo that returns a list with a single element,
because it corresponds to a single hyperparameter that is being tuned.
Suppose the class.weights hyperparameter should be tuned
along two dimensions: